IRR function
Simple IRR example | Present Values | IRR rule
Use the IRR function in Excel to calculate a project’s internal rate of return. The internal rate of return is the discount rate that makes the net present value equal to zero.
Simple IRR example
For example, project A requires an initial investment of $100 (cell B5).
1. We expect a profit of $0 at the end of the first period, a profit of $0 at the end of the second period and a profit of $152.09 at the end of the third period.
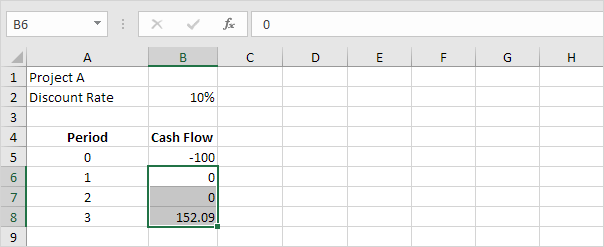
Note: the discount rate equals 10%. This is the rate of return of the best alternative investment. For example, you could also put your money in a savings account at an interest rate of 10%.
2. The correct NPV formula in Excel uses the NPV function to calculate the present value of a series of future cash flows and subtracts the initial investment.
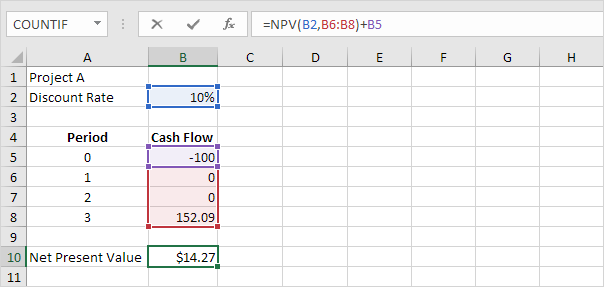
Explanation: a positive net present value indicates that the project’s rate of return exceeds the discount rate. In other words, it’s better to invest your money in project A than to put your money in a savings account at an interest rate of 10%.
3. The IRR function below calculates the internal rate of return of project A.
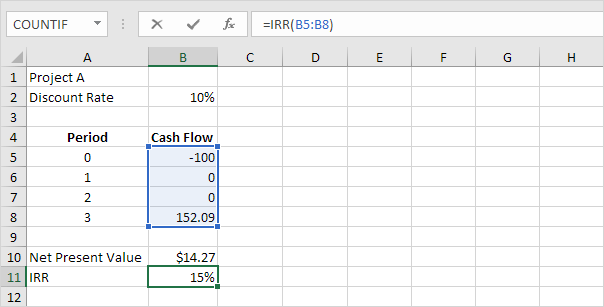
4. The internal rate of return is the discount rate that makes the net present value equal to zero. To clearly see this, replace the discount rate of 10% in cell B2 with 15%.
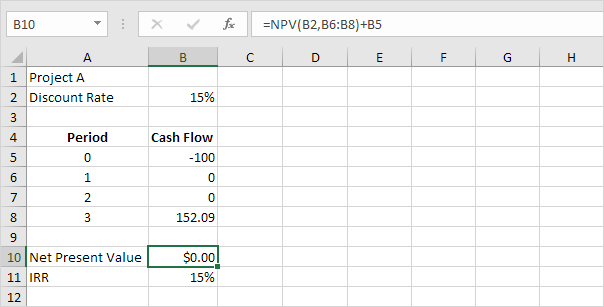
Explanation: a net present value of 0 indicates that the project generates a rate of return equal to the discount rate. In other words, both options, investing your money in project A or putting your money in a high-yield savings account at an interest rate of 15%, yield an equal return.
5. We can check this. Assume you put $100 into a bank. How much will your investment be worth after 3 years at an annual interest rate of 15%? The answer is $152.09.
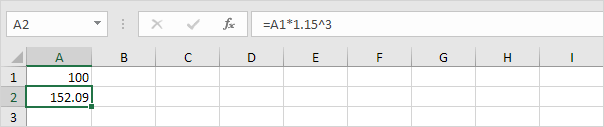
Conclusion: you can compare the performance of a project to a savings account with an interest rate equal to the IRR.
Present Values
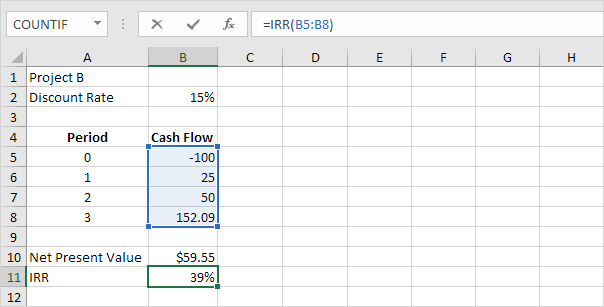
For example, project B requires an initial investment of $100 (cell B5). We expect a profit of $25 at the end of the first period, a profit of $50 at the end of the second period and a profit of $152.09 at the end of the third period.
1. The IRR function below calculates the internal rate of return of project B.
2. Again, the internal rate of return is the discount rate that makes the net present value equal to zero. To clearly see this, replace the discount rate of 15% in cell B2 with 39%.
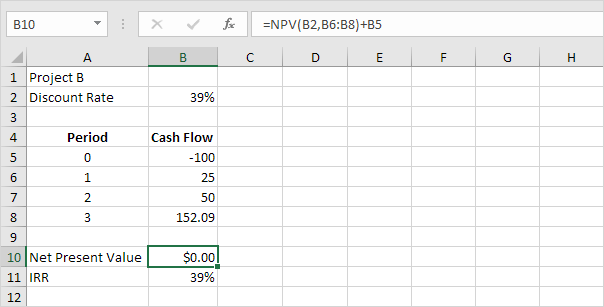
Explanation: a net present value of 0 indicates that the project generates a rate of return equal to the discount rate. In other words, both options, investing your money in project B or putting your money in a high-yield savings account at an interest rate of 39%, yield an equal return.
3. We can check this. First, we calculate the present value (pv) of each cash flow. Next, we sum these values.
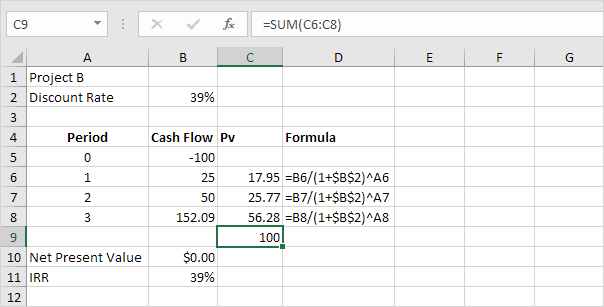
Explanation: instead of investing $100 in project B, you could also put $17.95 in a savings account for 1 year, $25.77 in a savings account for 2 years and $56.28 in a savings account for three years, at an annual interest rate equal to the IRR (39%).
IRR rule
The IRR rule states that if the IRR is greater than the required rate of return, you should accept the project. IRR values are frequently used to compare investments.
1. The IRR function below calculates the internal rate of return of project X.
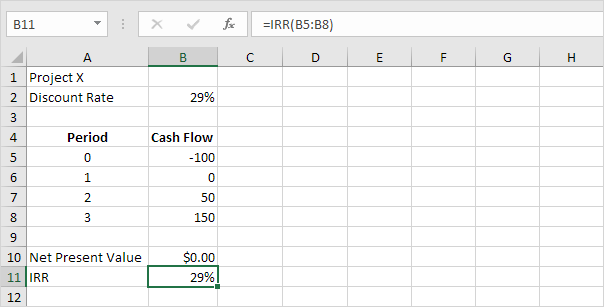
Conclusion: if the required rate of return equals 15%, you should accept this project because the IRR of this project equals 29%.
2. The IRR function below calculates the internal rate of return of project Y.
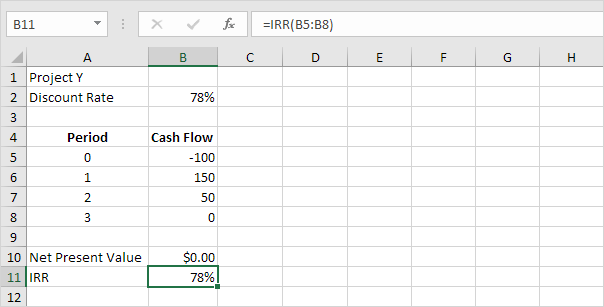
Conclusion: in general, a higher IRR indicates a better investment. Therefore, project Y is a better investment than project X.
3. The IRR function below calculates the internal rate of return of project Z.
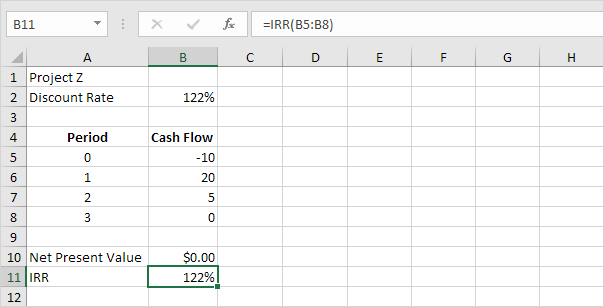
Conclusion: a higher IRR isn’t always better. Project Z has a higher IRR than project Y but the cash flows are much lower.
Next Chapter: Statistical Functions




