NPV
Net Present Value | Understanding the NPV function
The correct NPV formula in Excel uses the NPV function to calculate the present value of a series of future cash flows and subtracts the initial investment.
Net Present Value
For example, project X requires an initial investment of $100 (cell B5).
1. We expect a profit of $0 at the end of the first period, a profit of $50 at the end of the second period and a profit of $150 at the end of the third period.
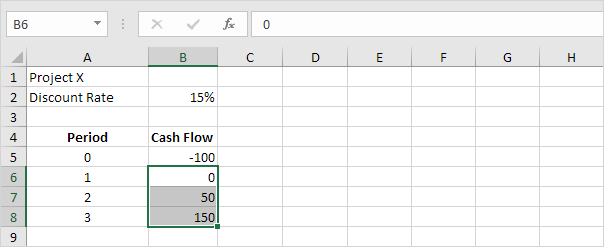
2. The discount rate equals 15%.

Explanation: this is the rate of return of the best alternative investment. For example, you could also put your money in a high-yield savings account at an interest rate of 15%.
3. The NPV formula below calculates the net present value of project X.
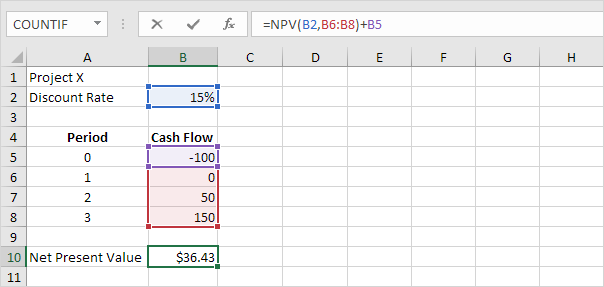
Explanation: a positive net present value indicates that the project’s rate of return exceeds the discount rate. In other words, it’s better to invest your money in project X than to put your money in a high-yield savings account at an interest rate of 15%.
4. The NPV formula below calculates the net present value of project Y.
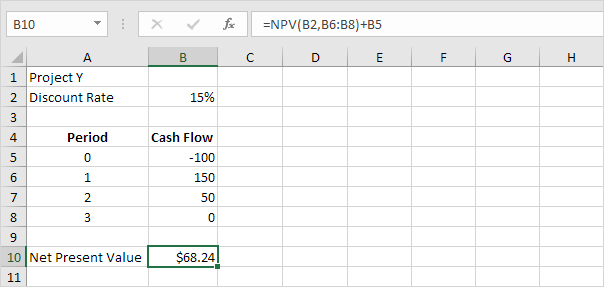
Explanation: the net present value of project Y is higher than the net present value of project X. Therefore, project Y is a better investment.
Understanding the NPV function
The NPV function simply calculates the present value of a series of future cash flows. This is not rocket science.
1. For example, project A requires an initial investment of $100 (cell B5). We expect a profit of $0 at the end of the first period, a profit of $0 at the end of the second period and a profit of $152.09 at the end of the third period.
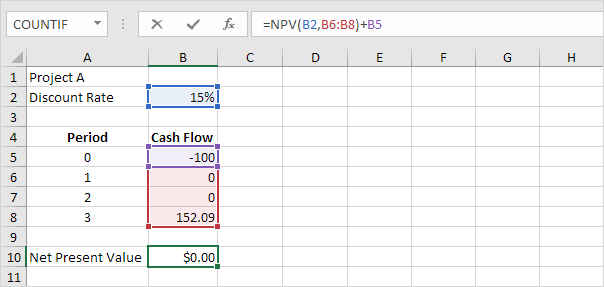
Explanation: a net present value of 0 indicates that the project generates a rate of return equal to the discount rate. In other words, both options, investing your money in project A or putting your money in a high-yield savings account at an interest rate of 15%, yield an equal return.
2. We can check this. Assume you put $100 into a bank. How much will your investment be worth after 3 years at an annual interest rate of 15%? The answer is $152.09.

Note: the internal rate of return of project A equals 15%. The internal rate of return is the discount rate that makes the net present value equal to zero. Visit our page about the IRR function to learn more about this topic.
3. The NPV function simply calculates the present value of a series of future cash flows.
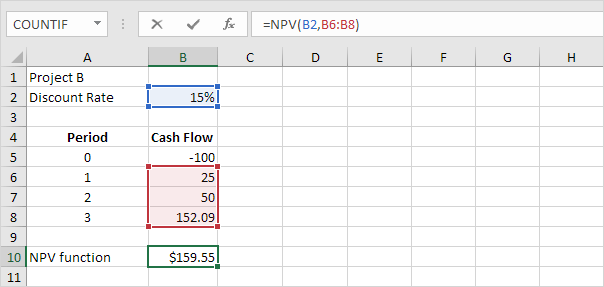
4. We can check this. First, we calculate the present value (pv) of each cash flow. Next, we sum these values.
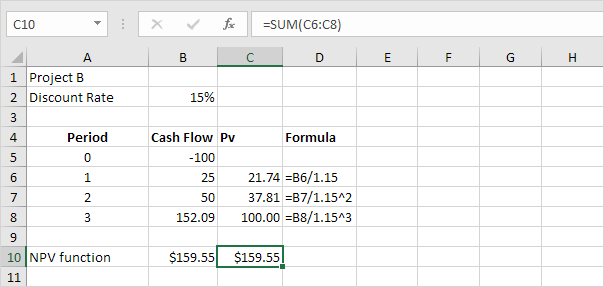
Explanation: $152.09 in 3 years is worth $100 right now. $50 in 2 years is worth 37.81 right now. $25 in 1 year is worth $21.74 right now. Would you trade $159.55 for $100 right now? Of course, so project B is a good investment.
5. The NPV formula below calculates the net present value of project B.
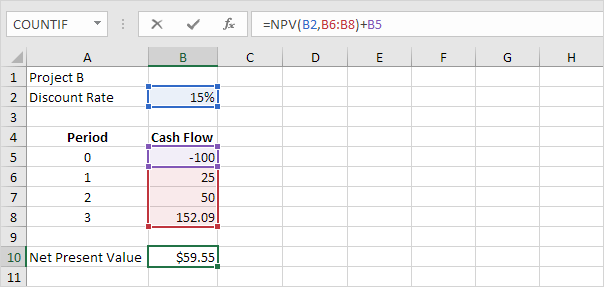
Explanation: project B is a good investment because the net present value ($159.55 – $100) is greater than 0.
Next Chapter: Statistical Functions




