Excel IRR formula
IRR refers to the Internal rate of return. Excel provides IRR formula to calculate the internal rate of return for a series of cash flows. This formula comes under the Excel Financial functions category. You can directly apply it to your Excel data and calculate the internal rate of return.
The IRR() function is very useful for calculating the internal rate of return and helpful in financial modeling. This chapter is going elaborate the IRR function, its usages, and examples to learn this function in detail. Just like the IRR, you have heard the term MIRR and XIRR.
How does IRR() function work?
There are three built-in functions in Excel to calculate the internal rate of return, IRR() is one of them. The users will be happy to know that – this function is available in all Excel versions. IRR() allows the users to calculate the internal rate of return and it returns the calculated result as a percentage value.
- Between all cash flows, there are always equal time intervals.
- Each time, the profit generated by the project is reinvested at the internal rate of return.
As we defined above, the IRR term refers to the Internal rate of return, where the term internal indicates that the IRR() function takes account only internal factors. Sometimes, it is also called as discount cash flow rate of return.
IRR() Syntax
Excel has the following syntax for the IRR() function that takes two arguments. One of which is required and another is an optional parameter.
Arguments
Values – Values parameter is an array of values that represent the series of cash flows. It is a required parameter and cash flow includes net income values and investment. Values parameter is provided as a range of cells. E.g., B2:B7
[guess] – It is another parameter that is optional to provide in the IRR() function. It is a number guessed by the user close to the expected IRR. Basically, it is an estimated value for the expected IRR. By default, it is .1 (means 10%).
Return Value
The IRR() function returns the internal rate of return. The value returned by this function is in the form of percentage, which means that it returns a percentage value.
Purpose
The purpose of using this function is to calculate the internal rate of return for a series of flows. The result return by this function is the form of percentage. It means that it returns a percentage value.
Tip: The user should be familiar with the mathematical version of IRR so that he/she can learn it easily and better.
Note
- The value parameter which is an array of values that must contain at least one positive and one negative value to calculate the IRR.
- Remember that – values inside the Values parameter should be in chronological order. It means it follows an order of values to interpret the cash flow.
- The IRR() function process only numbers inside Values parameters. Other types of values such as text, empty cells, or logical values are ignored.
- Sometimes when you use IRR() function, it returns the #NUM error. It occurs when –
- If the values for which you calculate the internal rate of return do not contain at least one positive and one negative value.
- The calculation fails after 20 iterations. If still, it is unable to find the result for internal rate of result, it returns #NUM error.
Limitation of IRR() function
IRR() function is a useful function to rate of return for assessing the capital projects. As the IRR() function is useful, but it also has a few limitations. These limitations are – Same reinvestment rate, Multiple results, and Relative measure.
These limitations are resolved by MIRR() and NVP functions.
- Same reinvestment rate
IRR has a problem: it always assumes that all cash flows generated by a project are reinvested at an equal rate to the IRR itself.
This issue is resolved by the MIRR() function, which refers to the Modified IRR. It allows the users to define the different reinvest rates and finance. - Multiple results
As we told you, there must be one positive and one negative value in alternative order that calculates more than one IRR. Just like the above limitation, this issue is solved by the alternative of IRR: MIRR() function. It is specially designed to produce only one rate. - Relative measure
Instead of considering the absolute values as a result, IRR() function considers percentage.
In this case, NPV is the solution for it. It is a better matrix than IRR because it considers the actual amount gained or lost by undertaking a project.
Examples of IRR() function
We will try to define each useful example that will help you to learn this function and make it easy for you to calculate the internal rate of return.
Suppose that we have taken the following data with initial investment and cash flows to calculate the internal rate of return using the Excel IRR() function.
| Period | Cash flow |
|---|---|
| Initial Investment | -$1000 |
| Month 1 | $300 |
| Month 2 | $400 |
| Month 3 | $500 |
| Calculated IRR | 8.90% |
Use the formula following formula =IRR(B2:B5)
Be sure that the Percentage formula is set for the cell where you will put or use the IRR() formula so that the result will display correctly. (Excel does this for you automatically.)
Now, implement this example in an Excel sheet and calculate the rate of return for this data.
Example 1
In this example, we will find out the internal rate of return for the given cash flow values using the IRR() function. Note that we are not providing the guess (the optional parameter) in this example.
Now, follow the steps carefully to learn the IRR() function and its working correctly.
Step 1: We have the following data that having initial investment and interval.
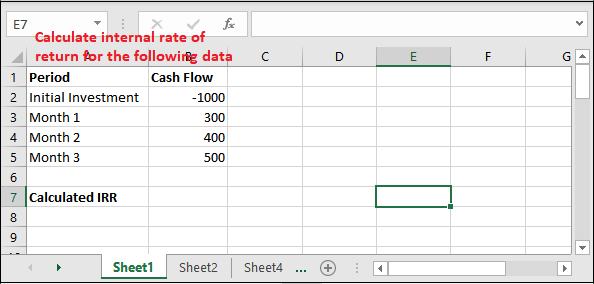
Here, one value is positive and another is negative.
Step 2: Go to an empty cell and write the IRR() formula with their arguments. For our dataset, the formula will be like –
=IRR(B2:B6)
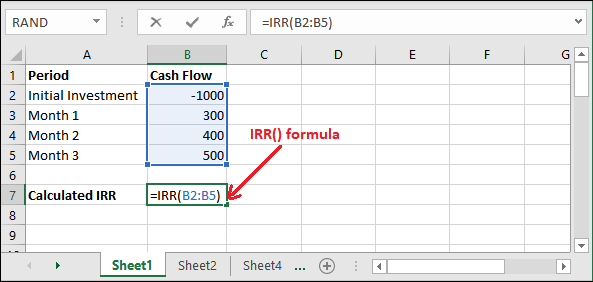
Step 3: Hit the Enter key and get the calculated IRR() returned a percentage value as a result.
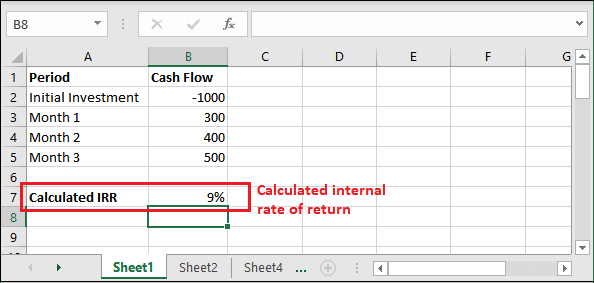
See that it has returned a value, i.e., 9%. It means the internal rate of return for the above data is 9%.
Example 2
We have taken another example with the same data used in the above example. But this time, we have changed the initial investment value to negative and now we will find out the internal rate of return for the given cash flow values using the IRR() function.
Now, follow the steps and see it will return #NUM! Error.
Step 1: We will now change all negative values to positive to see the result for it.
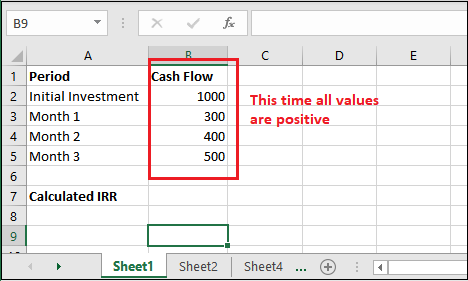
Step 2: Now, we will calculate the IRR for the same data, but this time initial investment is containing a positive number (1000).
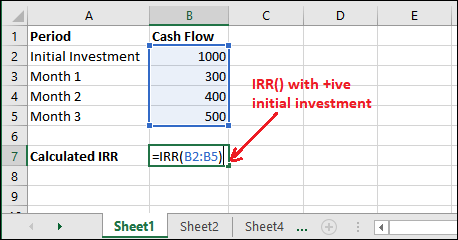
Step 3: See that it has returned #NUM! Error because at least one value must be negative and one positive.
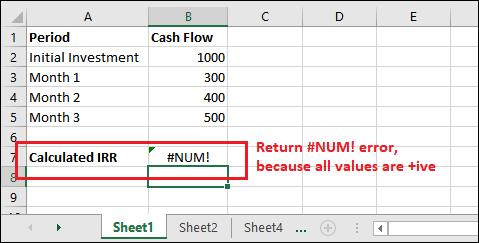
Example 3
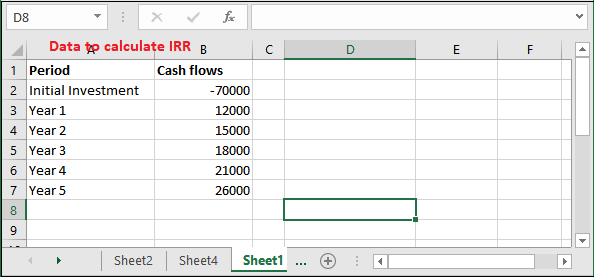
Now, take another example for calculating the internal rate of return to learn the IRR() function and leave no doubt about it. In this example, we will take an initial investment value 10 Lakhs and ten years income. Following are the steps to calculate the IRR –
Step 1: It is the data stored in an Excel sheet for this example where the initial investment is -70000 and for five years cash flows.
Step 2: For our dataset, the formula will be like –
=IRR(B2:B12)
Go to an empty cell and write the IRR() formula in it.
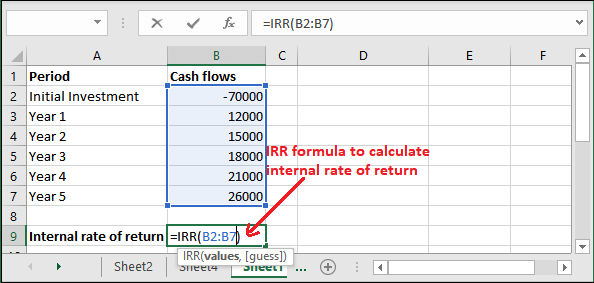
Step 3: Hit the Enter key and get the calculated IRR result as a percentage value.
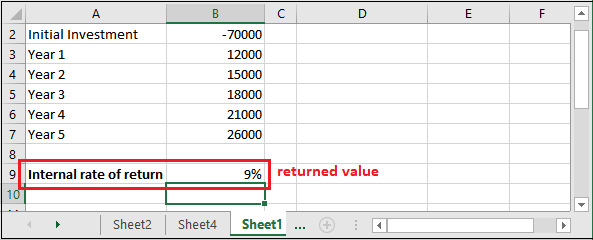
See that it has returned value a value, i.e., 9%. It means the internal rate of result for the above data is 9%.
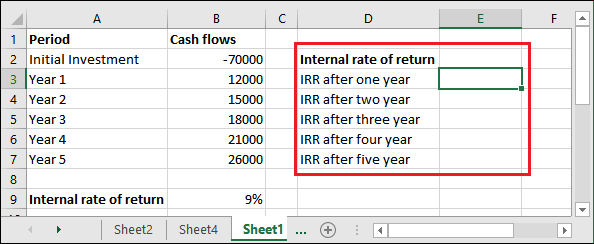
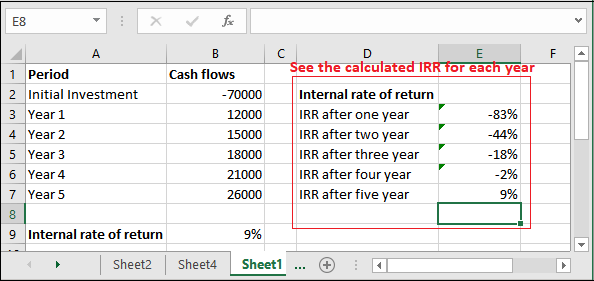
Step 4: Let’s try to calculate the internal rate of return after each year and see what it returns. So, we have designed a new column for it.
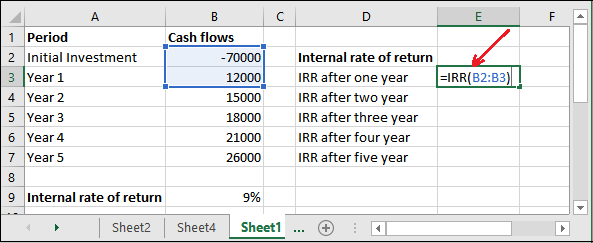
Step 5: Now, write down the given formula after a year of calculation along with the initial investment.
=IRR(B2:B3)
Step 6: It has returned the calculated IRR.
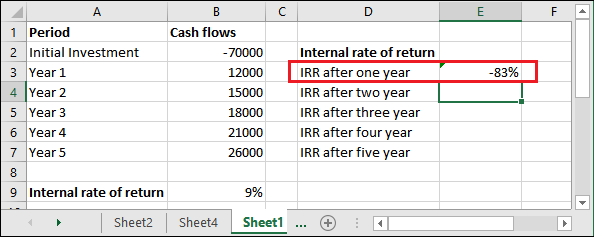
Now, similarly calculate the IRR for each year and see the result that we have calculated.
Essential terms of IRR() function
You have probably heard the term MIRR and XIRR, which come with some advanced functionality of IRR() function. They are also used to produce the rate of return. IRR() function has a few important terms that you should know while using these functions.
A negative and a positive cash flow value is required
All three functions, including IRR() require at least one positive and one negative cash flow value for calculation. Usually, the first number of your Excel data for calculating the rate of return is the negative number that usually refers to the initial investment.
Enter guess
Guess can be referred as the beginning rate from where the IRR() function starts calculating the internal rate of return incrementally. The IRR() function allows the users to enter the guess (expected value), as it is an optional parameter.
Excel allows the users to calculate up to 20 cycles for the IRR function until the result within 0.00001% is found. If the result is not found within the 20 iterations, Excel IRR() will generate the #NUM error.
If you don’t provide the guess
If you do not provide the guess, which is an optional parameter value in the IRR() function, Excel automatically assumes 0.1 (10%) as the initial guess.
Monthly v/s annual yields
If you want to calculate the IRR of monthly cash flow, the result must be multiplied by 12 to produce the annual yield. But if we talk about the XIRR function, it automatically produces the result for annual yield. So, the users do not require to multiply the result by 12 as the IRR() function.
You do not need to multiply the result by anything if you are calculating the IRR for annual cash flow yield.
#Num Error
IRR() function takes a guess parameter in which user can provide the expected value for the internal rate of return. If the returned result is not close to your defined expected value, this function return #NUM! Error.
In that case, Excel suggests the users to try again with the different expected values for guess.
Remark
IRR() function is very much similar to the NPV function that is a net present value.




